Statistiek betekenis p-waarde

De p-waarde (p-value) is een getal tussen 0 en 1, waarmee je bepaalt of een steekproefuitkomst statistisch significant is. Wanneer de p-waarde kleiner is dan het gekozen significantieniveau kun je stellen dat dat de gevonden uitkomst extreem genoeg is om je nulhypothese te verwerpen. Wat is de p-waarde? In de statistiek is de p-waarde (of p-waarde) de waarschijnlijkheid dat je een teststatistiek hebt verkregen, ervan uitgaande dat de nulhypothese waar is. Dat wil zeggen dat de p-waarde een waarde tussen 0 en 1 is die wordt gebruikt bij het testen van hypothesen om de nulhypothese te verwerpen of te accepteren. Statistiek betekenis p-waarde De -waarde geeft aan hoe extreem de gevonden waarde voor de toetsingsgrootheid in de verdeling onder de nulhypothese is. Hoe kleiner de p {\displaystyle p} -waarde, hoe extremer de uitkomst. In de praktijk worden waarden van 5% en 1% aangehouden als grens.

Significantie niveau

Het significantieniveau begrijpen (met voorbeelden) Gepubliceerd op 4 november door Julia erkt op 28 oktober Het significantieniveau (ook wel alfa, α, of level of significance genoemd) geeft de maximale kans weer dat je de nulhypothese ten onrechte verwerpt. Statistical significance dates to the 18th century, in the work of John Arbuthnot and Pierre-Simon Laplace, who computed the p-value for the human sex ratio at birth, assuming a null hypothesis of equal probability of male and female births; see p-value § History for details.

Significantie niveau Het significantieniveau kan ook hoger worden ingesteld voor significantietesten in niet-academische contexten, zoals voor marketingonderzoek of ander zakelijk onderzoek. Dit maakt het onderzoek minder streng en vergroot de kans dat je een statistisch significant resultaat vindt.

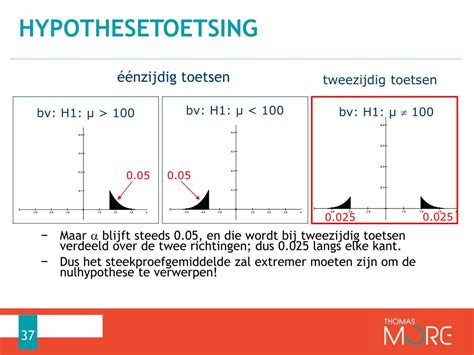
Hypothesetoetsing

Met hypothesetoetsing bereken je hoe waarschijnlijk het is dat een patroon of verband tussen onafhankelijke en afhankelijke variabelen door toeval zou kunnen zijn ontstaan. Bij kwantitatief onderzoek analyseer je de data door middel van hypothesetoetsing van de nulhypothese en alternatieve hypothese. Hypotheses: wat? Nulhypothese (H0): = Hypothese waartegen we bewijsmateriaal proberen vinden; die we willen verwerpen = Veelal: H0 ‘geen verschil’ of ‘geen effect’ vb. Ho = er is geen verschil tussen mannen en vrouwen voor wat betreft de tijd die ze gamen Alternatieve hypothese (Ha): = Hypothese.

Hypothesetoetsing Hypothesetoetsing! De H0 en de Ha Statistische toetsen worden onder andere gebruikt om de beredeneerde relatie tussen een invloedsfactor (X) en de afhankelijke variabele (Y) te toetsen.

Statistische relevantie

Andere soorten significantie en relevantie in onderzoek. Naast statistische significantie zijn ook klinische relevantie en praktische relevantie belangrijk. Praktische relevantie (ook wel praktische significantie genoemd) laat zien of de onderzoeksuitkomst belangrijk genoeg is om betekenisvol te zijn in de echte wereld. Voor deze vorm van. Statistische significantie is de zekerheid dat een uitkomst het gevolg is van een specifieke oorzaak en niet van toeval. Als een geobserveerd resultaat in data statistisch significant is, houdt dit in dat de kans groot is dat een specifieke factor of omstandigheid de uitkomst veroorzaakt.

Statistische relevantie Dikwijls wordt statistische significantie nog beschouwd als gelijkwaardig aan klinische relevantie. Aangezien een p-waarde een eenvoudige en dichotome maatstaf is voor het bekijken van toeval, biedt een p-waarde geen informatie over klinisch belang.

Kansberekening statistiek

Statistiek is het verzamelen/waarnemen en weergeven van getallen - bijvoorbeeld in tabellen en grafieken. Kansrekenen is daar een onderdeel van (met overigens vele onderdelen): je rekent met de getallen. Een kansberekening houdt zich bezig met situaties waarin toeval (mogelijk) een rol speelt. KANSREKENING EN STATISTIEK Jan van de Craats µ −σ µ +σ % µ −2σ µ +2σ % µ − 3σ µ +3σ % Collegedictaat – augustus Kansberekening statistiek Kansrekening is een belangrijk hulpmiddel in steekproeftheorie, statistiek en informatietheorie, met toepassingen in onder andere de natuurkunde, biologie, sociologie, psychologie en economie. Verdere achtergrond en onderbouwing van de axioma's van de kansrekening wordt gegeven in de maattheorie, die zich bezighoudt met het begrip 'maat', dat.